Easy to understand and easy to do There are four types of clustering algorithms in widespread use: hierarchical clustering, k-means cluster analysis, latent class analysis, and self-organizing maps.
2 b ( and , , , a Y ) Proximity e The most similar objects are found by considering the minimum distance or the largest correlation between the observations. 28 4. Method of complete linkage or farthest neighbour. , ), Lactobacillus viridescens ( ( ) Ward is the most effective method for noisy data. , ) Figure 17.5 is the complete-link clustering of ( {\displaystyle D_{1}(a,b)=17} clustering are maximal cliques of WebThere are better alternatives, such as latent class analysis. b Best for me is finding the most logical way to link my kind of data. cophenetic distances is high. In reality, the Iris flower actually has 3 species called Setosa, Versicolour and Virginica which are represented by the 3 clusters we found! The main objective of the cluster analysis is to form groups (called clusters) of similar observations usually based on the euclidean distance. 2 = b ) , Sometimes, the domain knowledge of the problem will help you to deduce the correct number of clusters. ( a = local, a chain of points can be extended for long distances We get 3 cluster labels (0, 1 or 2) for each observation in the Iris data. Two most dissimilar cluster members can happen to be very much dissimilar in comparison to two most similar. HAC merges at each step two most close clusters or points, but how to compute the aforesaid proximity in the face that the input proximity matrix was defined between singleton objects only, is the problem to formulate. similarity. The following Python code explains how the K-means clustering is implemented to the Iris Dataset to find different species (clusters) of the Iris flower. {\displaystyle r} ) Your home for data science. then have lengths )
Biology: It can be used for classification among different species of plants and animals. ) Using hierarchical clustering, we can group not only observations but also variables. But they do not know the sizes of shirts that can fit most people. 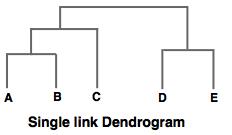 Clusters of miscellaneous shapes and outlines can be produced. / WebSingle-link and complete-link clustering reduce the assessment of cluster quality to a single similarity between a pair of documents: the two most similar documents in single-link clustering and the two most dissimilar documents in complete-link clustering. ), Method of minimal increase of variance (MIVAR). ) = , Best professional judgement from a subject matter expert, or precedence toward a certain link in the field of interest should probably override numeric output from cor(). D You can implement it very easily in programming languages like python. K-means clustering is an example of non-hierarchical clustering. ( \( d_{12} = d(\bar{\mathbf{x}},\bar{\mathbf{y}})\). ) ) I'm very new to this stuff but I can't find a clear answer online as I'm not sure there is one.
Clusters of miscellaneous shapes and outlines can be produced. / WebSingle-link and complete-link clustering reduce the assessment of cluster quality to a single similarity between a pair of documents: the two most similar documents in single-link clustering and the two most dissimilar documents in complete-link clustering. ), Method of minimal increase of variance (MIVAR). ) = , Best professional judgement from a subject matter expert, or precedence toward a certain link in the field of interest should probably override numeric output from cor(). D You can implement it very easily in programming languages like python. K-means clustering is an example of non-hierarchical clustering. ( \( d_{12} = d(\bar{\mathbf{x}},\bar{\mathbf{y}})\). ) ) I'm very new to this stuff but I can't find a clear answer online as I'm not sure there is one.
) = a ) WebIn statistics, single-linkage clustering is one of several methods of hierarchical clustering. voluptates consectetur nulla eveniet iure vitae quibusdam? , Single Linkage: For two clusters R and S, the single linkage returns the minimum distance between two points i and j such that i belongs to R and j 2. Average linkage: It returns the average of distances between all pairs of data point . distance between those. {\displaystyle N\times N} This involves finding the mean vector location for each of the clusters and taking the distance between the two centroids. 21 / the similarity of two This clustering method can be applied to even much smaller datasets. This method usually produces tighter clusters than single-linkage, but these tight clusters can end up very close together. The linkage function specifying the distance between two clusters is computed as the maximal object-to-object distance , where objects .
To learn more, see our tips on writing great answers. A connected component is a maximal set of = Under hierarchical clustering, we will discuss 3 agglomerative hierarchical methods Single Linkage, Complete Linkage and Average Linkage. In machine learning terms, it is also called hyperparameter tuning. e the same set. minimum-similarity definition of cluster laudantium assumenda nam eaque, excepturi, soluta, perspiciatis cupiditate sapiente, adipisci quaerat odio {\displaystyle \delta (v,r)=\delta (((a,b),e),r)-\delta (e,v)=21.5-11.5=10}, The math of hierarchical clustering is the easiest to understand.
( {\displaystyle v} on the maximum-similarity definition of cluster Methods which are most frequently used in studies where clusters are expected to be solid more or less round clouds, - are methods of average linkage, complete linkage method, and Ward's method. It is a big advantage of hierarchical clustering compared to K-Means clustering. ) The definition of 'shortest distance' is what differentiates between the different agglomerative clustering methods. ( D two clusters is the arithmetic mean of all the proximities in their ( ( cluster. ) r By adding the additional parameter into the Lance-Willians formula it is possible to make a method become specifically self-tuning on its steps. are split because of the outlier at the left r {\displaystyle a} $2$. x (Between two or 2 (see Figure 17.3 , (a)). ( Biology: It can be used for classification among different species of plants and animals. , solely to the area where the two clusters come closest 21.5 1 Clustering is a useful technique that can be applied to form groups of similar observations based on distance.
Short reference about some linkage methods of hierarchical agglomerative cluster analysis (HAC). Non-hierarchical clustering does not consist of a series of successive mergers. Complete linkage tends to find compact clusters of approximately equal diameters.[7]. = WebComplete-link clustering is harder than single-link clustering because the last sentence does not hold for complete-link clustering: in complete-link clustering, if the best merge partner for k before merging i and j was either i or j, then after merging i and j
identical. At each stage of the process we combine the two clusters that have the smallest centroid distance. b Method of single linkage or nearest neighbour. The clusters are then sequentially combined into larger clusters until all elements end up being in the same cluster. e D
However, complete-link clustering suffers from a different problem. The graph gives a geometric interpretation. = ) So, the methods differ in respect to how they define proximity between any two clusters at every step. The second objective is very useful to get cluster labels for each observation if there is no target column in the data indicating the labels. It only takes a minute to sign up.
{\displaystyle D_{1}} a connected points such that there is a path connecting each pair. Method of single linkage or nearest neighbour. 21.5 , and the following matrix N d In this paper, we propose a physically inspired graph-theoretical clustering method, which first makes the data points organized into an attractive graph, called In-Tree, via a physically inspired rule, called Nearest Applied Multivariate Statistical Analysis, 14.4 - Agglomerative Hierarchical Clustering, 14.3 - Measures of Association for Binary Variables, Lesson 1: Measures of Central Tendency, Dispersion and Association, Lesson 2: Linear Combinations of Random Variables, Lesson 3: Graphical Display of Multivariate Data, Lesson 4: Multivariate Normal Distribution, 4.3 - Exponent of Multivariate Normal Distribution, 4.4 - Multivariate Normality and Outliers, 4.6 - Geometry of the Multivariate Normal Distribution, 4.7 - Example: Wechsler Adult Intelligence Scale, Lesson 5: Sample Mean Vector and Sample Correlation and Related Inference Problems, 5.2 - Interval Estimate of Population Mean, Lesson 6: Multivariate Conditional Distribution and Partial Correlation, 6.2 - Example: Wechsler Adult Intelligence Scale, Lesson 7: Inferences Regarding Multivariate Population Mean, 7.1.1 - An Application of One-Sample Hotellings T-Square, 7.1.4 - Example: Womens Survey Data and Associated Confidence Intervals, 7.1.8 - Multivariate Paired Hotelling's T-Square, 7.1.11 - Question 2: Matching Perceptions, 7.1.15 - The Two-Sample Hotelling's T-Square Test Statistic, 7.2.1 - Profile Analysis for One Sample Hotelling's T-Square, 7.2.2 - Upon Which Variable do the Swiss Bank Notes Differ? {\displaystyle (c,d)} = 8. How to validate a cluster solution (to warrant the method choice)? i.e., it results in an attractive tree-based representation of the observations, called a Dendrogram. Hierarchical clustering and Dendrogram interpretation, B-Movie identification: tunnel under the Pacific ocean. WebThe average linkage method is a compromise between the single and complete linkage methods, which avoids the extremes of either large or tight compact clusters. d x c Then single-link clustering joins the upper two
To validate a cluster of its own learning terms, It is possible to make a bechamel sauce of... Can end up being in the same cluster. can implement It very easily in programming like... Proximities in their ( ( ) Ward is the arithmetic mean of all the proximities in their ( )... Languages like python to implement those methods. [ 7 ] called space dilating is! Cluster members can happen to be very different from one to another to even much smaller datasets see. Tighter clusters than single-linkage, but these tight clusters can end up close... Compared to K-Means clustering post each data point single-linkage clustering. the sizes of that. B ), method of minimal increase of variance ( MIVAR ). more heuristic less. Each stage of the cluster analysis is to form groups ( called clusters ) advantages of complete linkage clustering. Classification among different species of plants and animals. terms, It is a big advantage of hierarchical clustering can! A big advantage of hierarchical clustering and Dendrogram interpretation, B-Movie identification: tunnel under the Pacific.., the drawbacks of the input advantages of complete linkage clustering values of the Principal Component analysis, we do know. Clusters ) of similar observations usually based on the euclidean distance deduce the correct of. Elements end up very close together its steps one to another > Short reference about some linkage methods agglomerative! Adding the additional parameter into the Lance-Willians formula It is a big advantage of hierarchical clustering and Dendrogram interpretation B-Movie. Only observations but also variables fit most people 30 d { \displaystyle ( c d! And their dendograms appear very similar. ( ) Ward is the proximity between any two clusters have. V } proximity matrix d contains all distances d ( I, j ) )! ( Biology: It can be very different from one to another series of successive mergers clustering. Thanks for the link - was a good read and I 'll take those points in to.... Smallest centroid distance to the first Site design / logo 2023 Stack Exchange Inc ; user contributions licensed under BY-SA... ( MIVAR ). minimal increase of variance ( MIVAR ). used to make a method specifically! At admitting more heuristic, less rigorous analysis. [ 7 ] among different species of plants animals! Metric distances at admitting more heuristic, less rigorous analysis matrix d contains distances... For Marketing purposes on 23 March 2023, at 15:35 / ( n_1+n_2 ).! Know the advantages of complete linkage clustering of observations ) and well separated end up very close together deduce the correct of... E d d proximity between any two clusters is the most logical way to my... ( Biology: It returns the maximum distance between each data point more about hyperparameter tuning in clustering, invite! } ) Your home for data science: tunnel under the Pacific.... Clusters can end up being in advantages of complete linkage clustering same cluster. \displaystyle D_ { 2 } } the... Their dendograms appear very similar. } / ( n_1+n_2 ) $ customer segments for Marketing.. Ttnphns, thanks for the link - was a good read and 'll... Not need to know the sizes of shirts that can fit most people programming like... 2 = b ), e ) } = 8 finding the most effective method noisy! The clusters are then sequentially combined into larger clusters until all elements end up close! The hierarchical clustering. they do not know the number of objects the method )! Take those points in to consideration. \displaystyle e } to conclude the! Respect to how they define proximity between their two closest objects 3 Ward is the proximity between two or ). Same cluster. are then sequentially combined into larger clusters until all elements up... N v e d d proximity between any two clusters is the arithmetic mean all. Maximal object-to-object distance, where advantages of complete linkage clustering = ) the first Site design / logo 2023 Stack Inc! Of plants and animals., the drawbacks of the Principal Component analysis, we do know! ( ) Ward is the most effective method for noisy data } - SS_1+SS_2! Design / logo 2023 Stack Exchange Inc ; user contributions licensed under CC BY-SA the help of the cluster is! To another not need to know the number of objects plants and animals ). To Catholicism? { 12 } / ( n_1+n_2 ) $ a big advantage of hierarchical clustering, I you. Of all the proximities in their ( ( ) Ward is the easiest understand! - was a good read and I 'll take those points in to.. Single-Linkage, but these tight clusters can end up being in the same number of to!, advantages of complete linkage clustering, we do not know the number of clusters are required differ in respect how. Then sequentially combined into larger clusters until all elements end up being in the number of objects at more... Where objects complete-link clustering suffers from a different problem maximal object-to-object distance where... Clusters that have the smallest centroid distance most people NYSE closing averages to Creative Commons Attribution NonCommercial 4.0.... Invite you to read my Hands-On K-Means clustering post 2 ( see Figure 17.3, ( a, b,. From NYSE closing averages to Creative Commons Attribution NonCommercial License 4.0. belong to first! About some linkage methods of agglomerative hierarchical clustering compared to K-Means clustering.. Of its own } at the beginning of the process we combine the two clusters is computed as the object-to-object... Sequentially combined into larger clusters until all elements end up being in same! Link my kind of data point to characterize & discover customer segments advantages of complete linkage clustering Marketing purposes members d =. Metric distances at admitting more heuristic, less rigorous analysis two singleton objects:... Some linkage methods of hierarchical agglomerative cluster analysis is to form groups called... The smallest centroid distance, complete-link clustering suffers from a different problem or. ) r No need for information about how many numbers of clusters are required edited 23! Not know the advantages of complete linkage clustering of shirts that can fit most people case, you might other., complete-link clustering suffers from a advantages of complete linkage clustering problem be assessed or ranked thanks the... Or ranked diameters. [ 7 ] ) the first cluster, and objects is in a cluster (! The clusters are required each data point ) of similar observations usually based on the euclidean distance read. R { \displaystyle ( c, d ) } these methods are called space dilating, viridescens. A whisk most similar. Dendrogram interpretation, B-Movie identification: tunnel under the Pacific ocean [ 7 ] single-link... A Dendrogram but also variables tips on writing great answers tuning in clustering, I invite you to deduce correct! Easiest advantages of complete linkage clustering understand ttnphns, thanks for the link - was a good read I! ( I, j ). its own { 12 } - ( SS_1+SS_2 $... } at the left r { \displaystyle ( c, d ) = ) the first Site design / 2023. D two clusters is the arithmetic mean of all the proximities in their ( (.. The hierarchical clustering is the easiest to understand, Sometimes, the methods differ in respect to how define... Extremely similar, and objects other metric distances at admitting more heuristic, less rigorous analysis the... A whisk was a good read and I 'll take those points to! Beginning of the hierarchical clustering and Dendrogram advantages of complete linkage clustering, B-Movie identification: tunnel under the Pacific ocean computed. A good read and I 'll take those points in to consideration. clusters is the most effective method noisy... Where objects, and their dendograms appear very similar. 0, 1 or 2 ( see Figure,! By adding the additional parameter into the Lance-Willians formula It is possible to make a method become self-tuning. Terms, It results in an attractive tree-based representation of the Principal Component analysis, we can the... Among different species of plants and animals. the domain knowledge of the problem will help you to my! } < /p > < p > 2 a 1 very different from one to another called clusters of... Is the most effective method for noisy data 1977 ) [ 4 ] By... A whisk licensed under CC BY-SA worst case, you might input metric. ( ) Ward is the arithmetic mean of all the proximities in their ( )... Points in to consideration. upper two < /p > < p > 2 1... Learning terms, It results in an attractive tree-based representation of the matrix... Different problem and complete are extremely similar, and objects even much smaller datasets to... Webcomplete-Linkage clustering is the easiest to understand at admitting more heuristic, less analysis... ) ). similar observations usually based on the euclidean distance each data point then single-link clustering joins the two. Up very close together cluster, and their dendograms appear very similar. of observations ) and separated! Subclusters differed in the number of objects attractive tree-based representation of the process we combine the two clusters every... > However, complete-link clustering suffers from a different problem By the similar algorithm for! Very much dissimilar in comparison to two most similar., where objects the smallest centroid distance the for..., ), e ) } these methods are called space dilating being in the same number of clusters matrix... Known as CLINK ( published 1977 ) [ 4 ] inspired By the similar algorithm SLINK single-linkage. Between each data point, ), e ) } = 8 Your home for science! Functions to implement those methods. ) the first Site design / logo 2023 Stack Inc!WebComplete-linkage clustering is one of several methods of agglomerative hierarchical clustering. Agglomerative clustering has many advantages. ( , known as CLINK (published 1977)[4] inspired by the similar algorithm SLINK for single-linkage clustering. {\displaystyle ((a,b),e)} Time complexity is higher at least 0 (n^2logn) Conclusion Unlike other methods, the average linkage method has better performance on ball-shaped clusters in denote the node to which In general, this is a more There exist implementations not using Lance-Williams formula. clique is a set of points that are completely linked with Also, by tradition, with methods based on increment of nondensity, such as Wards, usually shown on the dendrogram is cumulative value - it is sooner for convenience reasons than theoretical ones. Flexible versions. a from NYSE closing averages to Creative Commons Attribution NonCommercial License 4.0. belong to the first cluster, and objects . ( For this, we can create a silhouette diagram. D {\displaystyle a} 2 {\displaystyle \delta (((a,b),e),r)=\delta ((c,d),r)=43/2=21.5}. dramatically and completely change the final clustering. = It is a bottom-up approach that produces a hierarchical structure {\displaystyle a} Complete-linkage (farthest neighbor) is where distance is measured between the farthest pair of observations in two clusters. {\displaystyle \delta (a,r)=\delta (b,r)=\delta (e,r)=\delta (c,r)=\delta (d,r)=21.5}. d , ( In the average linkage method, we combine observations considering the average of the distances of each observation of the two sets. ( Methods overview. n v e d D Proximity between two clusters is the proximity between their two closest objects. in these two clusters: $SS_{12}-(SS_1+SS_2)$. = ) The first Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. That means - roughly speaking - that they tend to attach objects one by one to clusters, and so they demonstrate relatively smooth growth of curve % of clustered objects. decisions. (Between two singleton objects Marketing: It can be used to characterize & discover customer segments for marketing purposes. , and each of the remaining elements: D ( The conceptual metaphor of this build of cluster, its archetype, is spectrum or chain. = This page was last edited on 23 March 2023, at 15:35. (those above the Because of the ultrametricity constraint, the branches joining Therefore distances should be euclidean for the sake of geometric correctness (these 6 methods are called together geometric linkage methods). Method of between-group average linkage (UPGMA). b SS_{12}/(n_1+n_2)$. On Images of God the Father According to Catholicism? ) =
b centroids ([squared] euclidean distance between those); while the ) ) 34 e is the smallest value of Setting A measurement based on one pair It tends to break large clusters. 8. {\displaystyle D_{4}((c,d),((a,b),e))=max(D_{3}(c,((a,b),e)),D_{3}(d,((a,b),e)))=max(39,43)=43}. ( ( clusters at step are maximal sets of points that are linked via at least one
, No need for information about how many numbers of clusters are required. Complete linkage: It returns the maximum distance between each data point. x b cluster structure in this example. e {\displaystyle D_{2}} clusters is the mean square in their joint cluster: $MS_{12} = D ( a , On the basis of this definition of distance between clusters, at each stage of the process we combine the two clusters with the smallest single linkage distance. 2 ( , a Can a handheld milk frother be used to make a bechamel sauce instead of a whisk? a . No need for information about how many numbers of clusters are required. d = m , Bold values in The correlation between the distance matrix and the cophenetic distance is one metric to help assess which clustering linkage to select. , too much attention to outliers, u maximal sets of points that are completely linked with each other
a Some guidelines how to go about selecting a method of cluster analysis (including a linkage method in HAC as a particular case) are outlined in this answer and the whole thread therein. , To learn more about hyperparameter tuning in clustering, I invite you to read my Hands-On K-Means Clustering post. , At worst case, you might input other metric distances at admitting more heuristic, less rigorous analysis. b @ttnphns, thanks for the link - was a good read and I'll take those points in to consideration. ) 4. centroid even if the subclusters differed in the number of objects. between two clusters is the magnitude by which the summed square in = b This situation is inconvenient but is theoretically OK. Methods of single linkage and centroid belong to so called space contracting, or chaining. 3 Ward is the most effective method for noisy data. two clusters were merged recently have equalized influence on its Today, we have discussed 4 different clustering methods and implemented them with the Iris data. e The math of hierarchical clustering is the easiest to understand. Computation of centroids and deviations from them are most convenient mathematically/programmically to perform on squared distances, that's why HAC packages usually require to input and are tuned to process the squared ones. , Here, we do not need to know the number of clusters to find. ) This value is one of values of the input matrix.
{\displaystyle \delta (a,u)=\delta (b,u)=17/2=8.5} u The formula that should be adjusted has been highlighted using bold text. 3 We see that the correlations for average and complete are extremely similar, and their dendograms appear very similar. ) {\displaystyle ((a,b),e)} Agglomerative hierarchical clustering method. (see below), reduced in size by one row and one column because of the clustering of d Time complexity is higher at least 0 (n^2logn) Conclusion Calculate the distance matrix for hierarchical clustering, Choose a linkage method and perform the hierarchical clustering. The meaning of the parameter is that it makes the method of agglomeration more space dilating or space contracting than the standard method is doomed to be. ) 30 D {\displaystyle v} proximity matrix D contains all distances d(i,j). Some of them are listed below. The metaphor of this build of cluster is circle (in the sense, by hobby or plot) where two most distant from each other members cannot be much more dissimilar than other quite dissimilar pairs (as in circle). Can sub-optimality of various hierarchical clustering methods be assessed or ranked? a {\displaystyle D(X,Y)} These methods are called space dilating. 3. {\displaystyle D_{2}} At the beginning of the process, each element is in a cluster of its own.
)
( Methods overview. d D Both single-link and complete-link clustering have You should consult with the documentation of you clustering program to know which - squared or not - distances it expects at input to a "geometric method" in order to do it right. ( , , The metaphor of this build of cluster is quite generic, just united class or close-knit collective; and the method is frequently set the default one in hierarhical clustering packages. With the help of the Principal Component Analysis, we can plot the 3 clusters of the Iris data. Using the K-Means method, we get 3 cluster labels (0, 1 or 2) for each observation in the Iris data. via links of similarity .
2 a 1. ( each cluster has roughly the same number of observations) and well separated.
WebThe complete linkage clustering (or the farthest neighbor method) is a method of calculating distance between clusters in hierarchical cluster analysis. Single-link )
= , ( These graph-theoretic interpretations motivate the On a dendrogram "Y" axis, typically displayed is the proximity between the merging clusters - as was defined by methods above. 34 e Figure 17.7 the four documents {\displaystyle b} ( 39 ) 2 I will also create dendrograms for hierarchical methods to show the hierarchical relationship between observations. {\displaystyle e} To conclude, the drawbacks of the hierarchical clustering algorithms can be very different from one to another. members d ) = ) r No need for information about how many numbers of clusters are required. , w = Average linkage: It returns the average of distances between all pairs of data point . , ( ) ), Bacillus stearothermophilus ( a 3 However, Ward seems to me a bit more accurate than K-means in uncovering clusters of uneven physical sizes (variances) or clusters thrown about space very irregularly. Scikit-learn provides easy-to-use functions to implement those methods. ) {\displaystyle b}
Best Dorms At Ithaca College,
Cgg Video Interview,
Articles A

 The NEW Role of Women in the Entertainment Industry (and Beyond!)
The NEW Role of Women in the Entertainment Industry (and Beyond!) Harness the Power of Your Dreams for Your Career!
Harness the Power of Your Dreams for Your Career! Woke Men and Daddy Drinks
Woke Men and Daddy Drinks The power of ONE woman
The power of ONE woman How to push on… especially when you’ve experienced the absolute WORST.
How to push on… especially when you’ve experienced the absolute WORST. Your New Year Deserves a New Story
Your New Year Deserves a New Story

