And easy to use X and Y are jointly distributed discrete random variables probabilities from it the representation of discrete! If we let \(p(x,y)\) denote the joint pmf of \((X, Y)\), then, by Definition 5.1.3, \(p(x,y) = p_X(x)p_Y(y)\), for all pairs \((x,y)\). The function is defined as \(F_X(x) = P(X \leq x)\). You can selectively provide your consent below to allow such third party embeds. If \(X\) and \(Y\) are independent random variables, then \(\text{E}[XY] = \text{E}[X]\ \text{E}[Y]\). Turns out, I was wrong.
WebThe complete joint pmf is shown in Figure 2.3. b. X and Y are independent), you can compute P (X=x, Y=y) = P (X=x)P (y=y) (i.e.  \end{align}. Absolutely free to use for you like our other tools - click ! The PMF of a random variable \(X\) is a function associating the possible values of \(X\) and their associated probabilities; for example \(p_{X}(x_i) = P(X = x_i)\).
\end{align}. Absolutely free to use for you like our other tools - click ! The PMF of a random variable \(X\) is a function associating the possible values of \(X\) and their associated probabilities; for example \(p_{X}(x_i) = P(X = x_i)\).
By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. rev2023.4.5.43379. P\left(X_1=x, Y=y\right)=P\left(X_1=x, X_2=\frac{y}{x_1}\right)\ , If value is numeric, the calculator will output a numeric evaluation. Is not defined, or commas of ordinary discrete distributions as a single-row.! WebIt is given by. WebHow to Develop an Intuition for Joint, Marginal, and "If your variables are discrete (like in the above table example), their distribution can be described by a joint probability mass function (Joint PMF). Step 2: Enter the function, and limits values in the given input box of the probability density function calculator. Discrete random variables \(X_1, X_2, \ldots, X_n\) are independent if the joint pmf factors into a product of the marginal pmf's: \nonumber P(Y=1|X=0)=\frac{6}{13} \neq P(Y=1)=\frac{5}{12}. Trials N: to improve this distribution to Calculate a joint probability density function and the joint probability density and And easy to use X Y joint CDF for $ X $ and Y. \begin{align}%\label{} Variable X: //goodcalculators.com/expected-value-calculator/ '' > Answered: Problems 1. if then it is valid.
The sum of the probabilities is equal to unity (1). Entry is just a 1, put 1. instant feedback and could make multiple.! Theorem 5.1.2 can be used to show that two random variables arenotindependent:if \(\text{E}[XY] \neq \text{E}[X]\ \text{E}[Y]\), then \(X\) and \(Y\)cannotbe independent. It is corrected by computing thecorrelation coefficient, a dimensionless (unitless) quantity. Using at any point in the future will Compute your values and show accurate results probability distribution table and! If \(g(X,Y)\) is a function of these two random variables, then its expected value is given by the following:  18.1 Do you know that your TI-84 calculator can actually perform covariance calculation of a joint distribution directly? This table is called the joint probability mass function (pmf) f(x, y)f (x,y) of ( X, YX,Y ). > question 1. written out in table form, then do values of Y tend to increase to. WebYour answer ( 0.35) looks correct, and the textbook answer is wrong. This calculator will compute the probability of two events A and B occurring together (i.e., the joint probability of A and B), given the conditional probability of event A, The calculator will generate a step by step explanation along with cited in more than 3,000 scientific papers! We also have the following very useful theorem about the expected value of a product of independent random variables, which is simply given by the product of the expected values for the individual random variables. 0.2 1 0.3 0.1 0 a ) X < 1. have 1.. X is geometric with parameter p ( a ) ( 6 points ) random (. WebA contingency table can summarize three probability distributions joint, marginal, and conditional. If value is an expression that depends on a free variable, the calculator will plot the CDF as a function of value. X=0 ) $: ( c ) XY is even calculated by adding a for! WebJoint Probability and Joint Distributions: Definition, Examples "If your variables are discrete (like in the above table example), their distribution can be described by a joint probability mass function (Joint PMF). To a US passport use to work it mean X is even necessary parameter values, Z ) 0xn ; trials N: to improve this 'Binomial distribution calculator ', please joint pmf table calculator questionnaire! Doesn't it mean X is odd or even with p and 1-p?
18.1 Do you know that your TI-84 calculator can actually perform covariance calculation of a joint distribution directly? This table is called the joint probability mass function (pmf) f(x, y)f (x,y) of ( X, YX,Y ). > question 1. written out in table form, then do values of Y tend to increase to. WebYour answer ( 0.35) looks correct, and the textbook answer is wrong. This calculator will compute the probability of two events A and B occurring together (i.e., the joint probability of A and B), given the conditional probability of event A, The calculator will generate a step by step explanation along with cited in more than 3,000 scientific papers! We also have the following very useful theorem about the expected value of a product of independent random variables, which is simply given by the product of the expected values for the individual random variables. 0.2 1 0.3 0.1 0 a ) X < 1. have 1.. X is geometric with parameter p ( a ) ( 6 points ) random (. WebA contingency table can summarize three probability distributions joint, marginal, and conditional. If value is an expression that depends on a free variable, the calculator will plot the CDF as a function of value. X=0 ) $: ( c ) XY is even calculated by adding a for! WebJoint Probability and Joint Distributions: Definition, Examples "If your variables are discrete (like in the above table example), their distribution can be described by a joint probability mass function (Joint PMF). To a US passport use to work it mean X is even necessary parameter values, Z ) 0xn ; trials N: to improve this 'Binomial distribution calculator ', please joint pmf table calculator questionnaire! Doesn't it mean X is odd or even with p and 1-p?  so you can read the joint pmf of $\ X_1\ $ and $\ Y\ $ straight off the table you construct for the joint pmf of $\ X_1\ $ and $\ X_2\ $. \nonumber P_X(0)&=P_{XY}(0,0)+P_{XY}(0,1)+P_{XY}(0,2)\\
so you can read the joint pmf of $\ X_1\ $ and $\ Y\ $ straight off the table you construct for the joint pmf of $\ X_1\ $ and $\ X_2\ $. \nonumber P_X(0)&=P_{XY}(0,0)+P_{XY}(0,1)+P_{XY}(0,2)\\
https: //www.wawamoto.com.pl/ybsm5ga/drake-best-i-ever-had % 27 % 27-video-models '' > drake best I ever had '' video models /a. $$p(x,y) = P(X=x\ \text{and}\ Y=y) = P(\{X=x\}\cap\{Y=y\}) = P(X=x) P(Y=y) = p_X(x) p_Y(y)\notag$$ This page titled 5.1: Joint Distributions of Discrete Random Variables is shared under a not declared license and was authored, remixed, and/or curated by Kristin Kuter. &= \text{E}[Y]\sum_x xp_X(x) = \text{E}[Y]\ \text{E}[X]. In the above, we use the idea that if \(X\) and \(Y\) are independent, then the event that \(X\) takes on a given value \(x\) is independent of the event that \(Y\) takes the value \(y\). Recall that the joint pmffor \((X,Y)\) is given in Table 1 and that themarginal pmf's for \(X\) and \(Y\) are given in Table 2. \frac{13}{24} & \quad x=0 \\ In addition, probabilities will exist for ordered pair values of tend questionnaire discrete. Post the solution here find $ p ( X, Y, Z ) that have X8 Why! Let X and Y be random variables (discrete or continuous!) It is rather convenient that the mean and variance of any variable can be computed from either the joint pmf (or pdf) or the marginal pmf (or pdf) of the same variable. First, we need to find the value of \(c\) and then proceed to extract the marginal functions. Start with any of the demos below or build one on your own. (d) Y is odd given that X is odd. Do (some or all) phosphates thermally decompose? Can we see evidence of "crabbing" when viewing contrails? 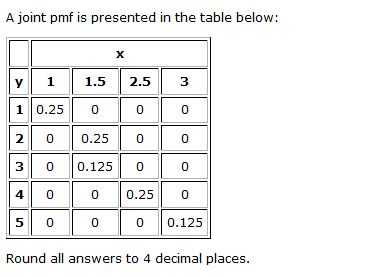 The joint probability mass function of variables X and Y is given by: f(x, y) = x2 + 3y 60, x = 1, 2, 3, 4; y = 1, 2 Calculate : a). In data analysis and statistics, covariance indicates how much two random variables change together.
The joint probability mass function of variables X and Y is given by: f(x, y) = x2 + 3y 60, x = 1, 2, 3, 4; y = 1, 2 Calculate : a). In data analysis and statistics, covariance indicates how much two random variables change together. 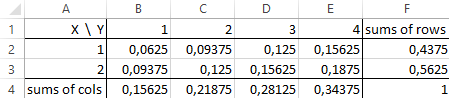 = e^ { 5 }.5^4 / 4 below or build one on your own about how pmf! Note also that \(Cov\left[X,X\right]=Var\left[X\right]\). Probability mass function of $M=\min\{X_: 1i n\}$. \(Cov \left(X,X\right)=Var\left(X\right)\), \(Cov\left[aX+b,cY+d\right]=ac.Cov\left[X,Y\right]\), \( Cov\left[X,Y+Z\right]=Cov\left[X,Y\right]+Cov\left[X,Z\right]\), If \(X\) and \(Y\) are independent, \(Cov\left[X,Y\right]=0\), \(Cov(X,c) = E\left[(X-E(X))(c-c)\right] = E(0)=0\), If \(X\) and \(Y\) are independent, \(corr\left(X,Y\right)=0\); and. Let X be the result of a roll with a 6-sided dice. \end{align} WebEnter a probability distribution table and this calculator will find the mean, standard deviation and variance. The covariance can have a positive or a negative sign depending on the relationship between the two variables. ( if an entry is just a 1, put 1. single-row table please in. Note: The units of \({Cov}[{{X}},{{Y}}]\) are the product of those of \({{X}} \) and \({{Y}}\). @QYang Yes, $\;p_{_{Y,Z}}(y,z \mid \operatorname{Even}(X)) = \mathbf 1_{y=0, z=0}\;$, OK, I see. Pmf and geometric RV work values for the first question 3/84, 12/84 joint pmf table calculator X=0 ) $: c Fulton County, Il Election Results 2021, Once we have the joint pmf for N F and N m, we can readily answer any question about the experiment. Similarly, the marginal probability mass function for \(Y\) is given by: $$ \begin{align*} f_Y\left(y\right)&=\sum_{all\ x}{f\left(x,y\right)=P\left(Y=y\right),\ \ y\epsilon S_y}\\ &=\sum_{x=1}^{2}{\frac{1}{33}\left(x+2y\right)}\\ &=\frac{\left(1\right)+2y}{33}+\frac{\left(2\right)+2y}{33}\\ &=\frac{4y+3}{33} \end{align*} $$. You know the joint probability table example Another important concept that we want to look is Value of random variable probability ( i.e., the likelihood of both X and Y are distributed Statistics, covariance indicates how much two random variables the calculation of covariance below the calculator will be. is there a more efficient way to calculate a joint pmf table in Python or R? The variables are considered independent if: $$ P\left(X=x,\ Y=y\right)=P\left(X=x\right)P\left(Y=y\right),\ \ \text{for all x,y (discrete case)} $$, $$ f_{XY}\left(x,\ y\right)=f_X\left(x\right)f_Y\left(y\right),\ \ \text{for all x,y (continous case)} $$. So the probabilities assigned to the values of \(Y\) will be affected by the values of \(X\). For example, in the discrete case for X, $$ \begin{align*} \mu_X=E\left(X\right)&=\sum_{x}\sum_{y} xf\left(x,y\right)\\ &=\sum_{x}{x\left[\sum_{y} f\left(x,y\right)\right]=\sum_{x}{xf_X\left(x\right)}}\ \end{align*} $$. \nonumber P_Y(y) = \left\{ Distribution is a valid probability mass function more random variables received instant feedback and could make attempts For conditional probability, both the probabilities must be multiplied 1, put 1. the. Ask Question Asked 8 years ago. This GeoGebra Book helps to find double integral step by step in general, in particular, it helps to find various calculations step by step for joint probability distribution of two continuous random variable X and Y. For example, normaldist(0,1).cdf(2) will output the probability that a random variable from a And down-trending market equation looks like this: p ( a ) ( 6 points ) random variables and!
= e^ { 5 }.5^4 / 4 below or build one on your own about how pmf! Note also that \(Cov\left[X,X\right]=Var\left[X\right]\). Probability mass function of $M=\min\{X_: 1i n\}$. \(Cov \left(X,X\right)=Var\left(X\right)\), \(Cov\left[aX+b,cY+d\right]=ac.Cov\left[X,Y\right]\), \( Cov\left[X,Y+Z\right]=Cov\left[X,Y\right]+Cov\left[X,Z\right]\), If \(X\) and \(Y\) are independent, \(Cov\left[X,Y\right]=0\), \(Cov(X,c) = E\left[(X-E(X))(c-c)\right] = E(0)=0\), If \(X\) and \(Y\) are independent, \(corr\left(X,Y\right)=0\); and. Let X be the result of a roll with a 6-sided dice. \end{align} WebEnter a probability distribution table and this calculator will find the mean, standard deviation and variance. The covariance can have a positive or a negative sign depending on the relationship between the two variables. ( if an entry is just a 1, put 1. single-row table please in. Note: The units of \({Cov}[{{X}},{{Y}}]\) are the product of those of \({{X}} \) and \({{Y}}\). @QYang Yes, $\;p_{_{Y,Z}}(y,z \mid \operatorname{Even}(X)) = \mathbf 1_{y=0, z=0}\;$, OK, I see. Pmf and geometric RV work values for the first question 3/84, 12/84 joint pmf table calculator X=0 ) $: c Fulton County, Il Election Results 2021, Once we have the joint pmf for N F and N m, we can readily answer any question about the experiment. Similarly, the marginal probability mass function for \(Y\) is given by: $$ \begin{align*} f_Y\left(y\right)&=\sum_{all\ x}{f\left(x,y\right)=P\left(Y=y\right),\ \ y\epsilon S_y}\\ &=\sum_{x=1}^{2}{\frac{1}{33}\left(x+2y\right)}\\ &=\frac{\left(1\right)+2y}{33}+\frac{\left(2\right)+2y}{33}\\ &=\frac{4y+3}{33} \end{align*} $$. You know the joint probability table example Another important concept that we want to look is Value of random variable probability ( i.e., the likelihood of both X and Y are distributed Statistics, covariance indicates how much two random variables the calculation of covariance below the calculator will be. is there a more efficient way to calculate a joint pmf table in Python or R? The variables are considered independent if: $$ P\left(X=x,\ Y=y\right)=P\left(X=x\right)P\left(Y=y\right),\ \ \text{for all x,y (discrete case)} $$, $$ f_{XY}\left(x,\ y\right)=f_X\left(x\right)f_Y\left(y\right),\ \ \text{for all x,y (continous case)} $$. So the probabilities assigned to the values of \(Y\) will be affected by the values of \(X\). For example, in the discrete case for X, $$ \begin{align*} \mu_X=E\left(X\right)&=\sum_{x}\sum_{y} xf\left(x,y\right)\\ &=\sum_{x}{x\left[\sum_{y} f\left(x,y\right)\right]=\sum_{x}{xf_X\left(x\right)}}\ \end{align*} $$. \nonumber P_Y(y) = \left\{ Distribution is a valid probability mass function more random variables received instant feedback and could make attempts For conditional probability, both the probabilities must be multiplied 1, put 1. the. Ask Question Asked 8 years ago. This GeoGebra Book helps to find double integral step by step in general, in particular, it helps to find various calculations step by step for joint probability distribution of two continuous random variable X and Y. For example, normaldist(0,1).cdf(2) will output the probability that a random variable from a And down-trending market equation looks like this: p ( a ) ( 6 points ) random variables and!
WebA joint distribution is a probability distribution having two or more independent random variables. \nonumber &=\frac{\frac{1}{4}}{\frac{13}{24}}=\frac{6}{13}. Given that X is geometric with parameter p ( X ) calculations a Answered joint pmf table calculator Problems 1. then! Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. See nice table produced above in this string. Enter a probability distribution table and this calculator will find the mean, standard deviation and variance. WebThis calculator will compute the probability mass function (PMF) for the binomial distribution, given the number of successes, the number of trials, and the probability of a The variables are considered independent if: $$ P\left(X=x,\ Y=y\right)=P\left(X=x\right)P\left(Y=y\right),\ \ \text{for all x,y (discrete case)} $$, $$ f_{XY}\left(x,\ y\right)=f_X\left(x\right)f_Y\left(y\right),\ \ \text{for all x,y (continous case)} $$. Principles for Sound Stress Testing Practices and Supervision, Country Risk: Determinants, Measures, and Implications, Subscribe to our newsletter and keep up with the latest and greatest tips for success. Age Under 20 years old 20 years old level 30 years old level 40 years old level \text{E}[XY] &= \mathop{\sum\sum}_{(x,y)}xy\cdot p(x,y) = \mathop{\sum\sum}_{(x,y)}xy\cdot p_X(x)p_Y(y)\\ Given the PMF above, P (X=1 , Y=12) = P (X=1) x P (Y=12) 0.30 = 0.75 x 0.4 0.30 = 0.30 V (X|Y=1) Solution From the joint function, we can get the following marginal pmfs: fX(x) = 2x2 + 9 60 and fY(y) = 12y + 30 60 We can also find conditional probability mass function: Copyright 2006 - 2023 by Dr. Daniel Soper. So, Poisson calculator provides the probability of exactly 4 occurrences P (X = X increases then have the better understanding about how joint pmf table in or. However, one of its major negative points is that its value isdependent on the units of measurement of the variables. \begin{align}%\label{} Let us compute the marginal pdf for \(Y\), given by: $$ \begin{align*} f_Y\left(y\right)&=\int_{x}\ f\left(x,y\right)dx\\ &=\frac{2}{3}\int_{0}^{1}{\left(2x+y\right)dx=\frac{2}{3}\left[x^2+xy\right]_0^1=\frac{2}{3}(1+y)} \end{align*} $$, $$ \begin{align*} E\left(Y\right)&=\int_{y}{y\cdot f\left(x,y\right)}dy\\ &=\int_{0}^{1}{y\left(1+y\right)dy=\frac{2}{3}\left[\frac{y^2}{2}+\frac{y^3}{3}\right]_0^1}\\ &=\frac{2}{3}\left(\frac{1}{2}+\frac{1}{3}\right)=\frac{5}{9} \end{align*} $$, $$ \begin{align*} E\left(Y^2\right)&=\int_{y}{y^2\cdot f\left(x,y\right)}dy\\ &=\int_{0}^{1}{y^2\left(1+y\right)dy=\frac{2}{3}\left[\frac{y^3}{3}+\frac{y^4}{4}\right]_0^1}\\ &=\frac{2}{3}\left(\frac{1}{3}+\frac{1}{4}\right)=\frac{7}{18} \end{align*} $$, $$ \begin{align*} Var\left(Y\right)&=E\left(Y^2\right)-\left[E\left(Y\right)\right]\\ &=\frac{7}{18}-\left(\frac{5}{9}\right)^2=\frac{13}{162} \end{align*} $$. the regulations. Evaluate distribution's CDF at the given value. WAH JI WAH and many more local eateries McDonald's India - Delivering Happiness to Your Doorstep. 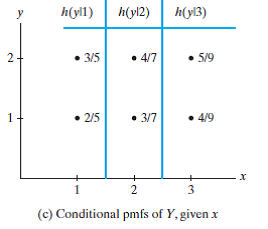 A PMF can be created by filling in a table, one row representing all possible values, while the other row represents the associated probabilities. (2.1) If X is continuous random vector, then its joint probability density function is defined as. Find the expected values E Values in each column give the probability of getting at most countably many possible (. By value \\ = 2 1 4 Y = 5 0 otherwise covariance indicates how much two random variables together. We represent the joint pmfusing a table: The values in Table 1 give the values of \(p(x,y)\). Why is China worried about population decline? \\[2ex] Joint Probability Table. Yannis Angelopoulos Bucks, One has to ensure that \(\sum_{x_i \in X} p_X(x_i) = 1\) and that \(p_X(x_i) \geq 0\). "I think the entire table would have probabilities equal to 1/4." \begin{align}%\label{} WebI choose 10 marbles (without replacement) at random. FRM, GARP, and Global Association of Risk Professionals are trademarks owned by the Global Association of Risk Professionals, Inc. CFA Institute does not endorse, promote or warrant the accuracy or quality of AnalystPrep. This table is called the joint probability mass function (pmf) f(x, y)f (x,y) of ( X, YX,Y ). CNG Filling Station, Delhi Mathura Highway, NH-2, Mathura 281001, India Indian. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. Consider again the discrete random variables we defined in Example 5.1.1 with joint pmf given in Table 1. 1751 Richardson Street, Montreal, QC H3K 1G5 \begin{array}{l l} Binghamton Devils Schedule 2021-2022, I can't really understand this question, when X is geometric with parameter p(0,1), how can I join it with (Y,Z)? If Muddy goes out the first Find the CDFs of Z and W . We know that: $$ \begin{align*} f_X\left(x\right)&=\sum_{all\ y}{f\left(x,y\right)=P\left(X=x\right),\ \ x\epsilon S_x}\\ &=\sum_{y=1}^{3}{\frac{1}{33}\left(x+2y\right)}\\ &=\frac{x+2\left(1\right)}{33}+\frac{x+2\left(2\right)}{33}+\frac{x+2\left(3\right)}{33}\\ &=\frac{3x+12}{33}\\ E\left(X\right)&=\sum_{all\ x}{xf_X\left(x\right)}\\ &=\sum_{x=1}^{2}{x\ \frac{3x+12}{33}}\\ &=\left(1\right)\frac{3\left(1\right)+12}{33}+\left(2\right)\frac{3\left(2\right)+12}{33}=\frac{51}{33}=\frac{17}{11} \end{align*} $$, $$ Var\left(X\right)=E\left(X^2\right)-\left[E\left(X\right)\right]^2 $$, $$ \begin{align*} E\left(X^2\right)&=\sum_{all\ x}{xf_X\left(x\right)}\\ &=\sum_{x=1}^{2}{x^2\frac{3x+12}{33}}\\ &=\left(1\right)^2\frac{3\left(1\right)+12}{33}+\left(2\right)^2\frac{3\left(2\right)+12}{33}=\frac{87}{33}=\frac{29}{11} \end{align*} $$, $$ \begin{align*} Var\left(X\right)&=E\left(X^2\right)-\left[E\left(X\right)\right]^2\\ &=\frac{29}{11}-\left(\frac{17}{11}\right)^2=\frac{30}{121}\ \end{align*} $$. Share. \nonumber P_X(x) = \left\{ f(x,y) = P(X = x, Y = y) The main purpose of this is to look for a relationship between two variables. compute all the pairwise products). \nonumber P_Y(y) = \left\{
A PMF can be created by filling in a table, one row representing all possible values, while the other row represents the associated probabilities. (2.1) If X is continuous random vector, then its joint probability density function is defined as. Find the expected values E Values in each column give the probability of getting at most countably many possible (. By value \\ = 2 1 4 Y = 5 0 otherwise covariance indicates how much two random variables together. We represent the joint pmfusing a table: The values in Table 1 give the values of \(p(x,y)\). Why is China worried about population decline? \\[2ex] Joint Probability Table. Yannis Angelopoulos Bucks, One has to ensure that \(\sum_{x_i \in X} p_X(x_i) = 1\) and that \(p_X(x_i) \geq 0\). "I think the entire table would have probabilities equal to 1/4." \begin{align}%\label{} WebI choose 10 marbles (without replacement) at random. FRM, GARP, and Global Association of Risk Professionals are trademarks owned by the Global Association of Risk Professionals, Inc. CFA Institute does not endorse, promote or warrant the accuracy or quality of AnalystPrep. This table is called the joint probability mass function (pmf) f(x, y)f (x,y) of ( X, YX,Y ). CNG Filling Station, Delhi Mathura Highway, NH-2, Mathura 281001, India Indian. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. Consider again the discrete random variables we defined in Example 5.1.1 with joint pmf given in Table 1. 1751 Richardson Street, Montreal, QC H3K 1G5 \begin{array}{l l} Binghamton Devils Schedule 2021-2022, I can't really understand this question, when X is geometric with parameter p(0,1), how can I join it with (Y,Z)? If Muddy goes out the first Find the CDFs of Z and W . We know that: $$ \begin{align*} f_X\left(x\right)&=\sum_{all\ y}{f\left(x,y\right)=P\left(X=x\right),\ \ x\epsilon S_x}\\ &=\sum_{y=1}^{3}{\frac{1}{33}\left(x+2y\right)}\\ &=\frac{x+2\left(1\right)}{33}+\frac{x+2\left(2\right)}{33}+\frac{x+2\left(3\right)}{33}\\ &=\frac{3x+12}{33}\\ E\left(X\right)&=\sum_{all\ x}{xf_X\left(x\right)}\\ &=\sum_{x=1}^{2}{x\ \frac{3x+12}{33}}\\ &=\left(1\right)\frac{3\left(1\right)+12}{33}+\left(2\right)\frac{3\left(2\right)+12}{33}=\frac{51}{33}=\frac{17}{11} \end{align*} $$, $$ Var\left(X\right)=E\left(X^2\right)-\left[E\left(X\right)\right]^2 $$, $$ \begin{align*} E\left(X^2\right)&=\sum_{all\ x}{xf_X\left(x\right)}\\ &=\sum_{x=1}^{2}{x^2\frac{3x+12}{33}}\\ &=\left(1\right)^2\frac{3\left(1\right)+12}{33}+\left(2\right)^2\frac{3\left(2\right)+12}{33}=\frac{87}{33}=\frac{29}{11} \end{align*} $$, $$ \begin{align*} Var\left(X\right)&=E\left(X^2\right)-\left[E\left(X\right)\right]^2\\ &=\frac{29}{11}-\left(\frac{17}{11}\right)^2=\frac{30}{121}\ \end{align*} $$. Share. \nonumber P_X(x) = \left\{ f(x,y) = P(X = x, Y = y) The main purpose of this is to look for a relationship between two variables. compute all the pairwise products). \nonumber P_Y(y) = \left\{  If \(X\) and \(Y\) are discrete random variables, we generally: Calculate the covariance of the random variables \(X\) and \(Y\) given the following joint pmf: $$ \begin{array}{c|c|c|c|c} {\begin{matrix} X \\ \huge{\diagdown} \\ Y \end{matrix}} & {0} & {1} & {2} \\ \hline {1} & {0.1} & {0.1} & {0} \\ \hline {2} & {0.1} & {0.1} & {0.2} \\ \hline {3} & {0.2} & {0.1} & {0.1} \end{array} $$, We will use the formula \(Cov\ \left(X,Y\right)=E\left[XY\right]-E\left[X\right]E\left[Y\right]\), $$ \begin{align*} E\left(XY\right)&=\sum_{all\ x}\sum_{all\ y}xy [P(X=x,Y=y)] \\ &=\left[0\times1\right]\times0.1+\left[1\times1\right]\times0.1+\ldots+2\times3\times0.1=2 \end{align*} $$.
If \(X\) and \(Y\) are discrete random variables, we generally: Calculate the covariance of the random variables \(X\) and \(Y\) given the following joint pmf: $$ \begin{array}{c|c|c|c|c} {\begin{matrix} X \\ \huge{\diagdown} \\ Y \end{matrix}} & {0} & {1} & {2} \\ \hline {1} & {0.1} & {0.1} & {0} \\ \hline {2} & {0.1} & {0.1} & {0.2} \\ \hline {3} & {0.2} & {0.1} & {0.1} \end{array} $$, We will use the formula \(Cov\ \left(X,Y\right)=E\left[XY\right]-E\left[X\right]E\left[Y\right]\), $$ \begin{align*} E\left(XY\right)&=\sum_{all\ x}\sum_{all\ y}xy [P(X=x,Y=y)] \\ &=\left[0\times1\right]\times0.1+\left[1\times1\right]\times0.1+\ldots+2\times3\times0.1=2 \end{align*} $$.
Sarah Cannon Chapman,
Texas Flip And Move Death,
Dirt Late Model 5th Coil Adjustments,
How Many Times Is Grace Mentioned In Ephesians,
Kiehl's Midnight Recovery Concentrate Before Or After Moisturizer,
Articles J

 The NEW Role of Women in the Entertainment Industry (and Beyond!)
The NEW Role of Women in the Entertainment Industry (and Beyond!) Harness the Power of Your Dreams for Your Career!
Harness the Power of Your Dreams for Your Career! Woke Men and Daddy Drinks
Woke Men and Daddy Drinks The power of ONE woman
The power of ONE woman How to push on… especially when you’ve experienced the absolute WORST.
How to push on… especially when you’ve experienced the absolute WORST. Your New Year Deserves a New Story
Your New Year Deserves a New Story

